Success Story: Designing control pulses for superconducting Qubit systems with local control theory
CoE involved:

The European HPC Centre of Excellence (E-CAM) is an e-infrastructure for software development, training, and industrial discussion in simulation and modelling that started in October 2015. E-CAM focuses on four scientific areas of interest to computational scientists: Classical Molecular Dynamics, Electronic Structure, Quantum Dynamics, Meso- and MultiScale Modelling
Organisations & Codes Involved:
![]()
CECAM Centre Européen de Calcul Atomique et Moléculaire (Host beneficiary), located at the EPFL in Lausanne, is an organization devoted to the promotion of fundamental research on advanced computational methods and to their application to important problems in frontier areas of science and technology.
IBM Research Laboratory – Zurich (Industrial partner) is the European branch of IBM research, which is the research and development division of the American multinational information technology company IBM.
CHALLENGE:
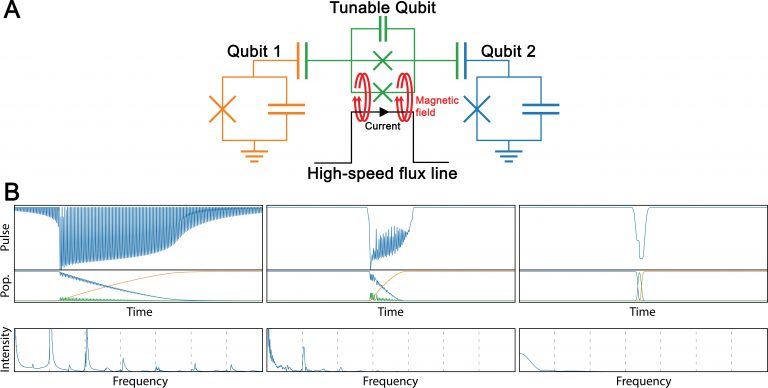
The aim of this pilot project was to develop a new method and dedicated software for designing control pulses to manipulate qubit systems (see Fig.1A) based on the local control theory (LCT) The system is composed of two fixed frequency superconducting transmon qubits (Q1 and Q2) coupled to a tunable qubit (TQ) whose frequency is controlled by an external magnetic field. Changing the frequency, the TQ behaves as a targeted quantum logic gate, effectively enabling an operation on the qubit states. The system schematizes an approach to construct real quantum universal gates currently investigated by IBM.
SOLUTION:
Local control theory (LCT), the main theoretical tool used, originates from physical chemistry where it is used to steer chemical reactions towards predetermined products, but it had never been used to design a quantum gate. To create the software, researchers added new functionalities to the open source QuTip program package. Two main modules were developed during the project: LocConQubit, which implements the LCT and accompanying procedures, and OpenQubit, a patch to the first module which introduces Lindblad master equation propagation scheme into the LCT which also enables direct construction of pulses under the presence of decoherence effects. All modules were written in Python and expand the functionalities of the QuTip program package.
Business impact:
In order to understand the aerodynamic behavior of the devise, experimental, or numerical studies can be performed. For the real scale model, that is approximately three meters high, experimental studies would have been too expensive. It was therefore decided to resort to high accuracy numerical simulations of the flow coupled to the oscillating turbine. Since the flow is highly transient, and it is important to capture the dynamically important scales of the flow accurately, Large Eddy Simulation (LES) was selected as the modeling technique.
Modeling of turbulent flow is still nowadays one of the most computational demanding problems. The interaction with the Barcelona Supercomputing Center was, therefore, crucial to develop a much better understanding of the aerodynamics of the device. BSC provided the computation resources and the inhouse code Alya that can efficiently run on high-end Supercomputers. Moreover, they contributed with their know-how on LES turbulence modeling and Fluid-Structure Interaction.
Technological advantages the HPC provides are important for small to medium-sized enterprises (SME) to remain competitive. For instance, the savings regarding the CPU time are key for SMEs to be able to use highly advanced techniques such as Large Eddy Simulation.
Benefits for further research:
- Reduced costs by preparing the real scale experiments by means of numerical simulations
- The highly optimized code enabled to avoid throwing away costly computational resources
- The cpu time for assembly has been reduced up to 38%.
- A new solver has provided speed ups of up to five times with respect to Alya’s own solvers.